How to Read a Sensitivity Report in Linear Programming
All MBA students will see linear programing in one or more than operations management courses in business school. Performing a linear programing model is one claiming. Interpreting the linear programing model'south solver reports nowadays another claiming. Solver reports include a Sensitivity Report, an Answer Report and a Limits Written report. This commodity shows yous how to translate a linear programing model's Sensitivity Report, Respond Report and Limits Study.
Nosotros will expect at the Answer Report, Sensitivity Study and Limits Written report one past i starting with the Sensitivity Report.
Interpreting the Sensitivity Report
The Sensitivity Study is the well-nigh useful of the iii reports. Information technology is very useful for managerial decisions. The sensitivity report is broken downwards into two parts. The variable cells and constraints section.
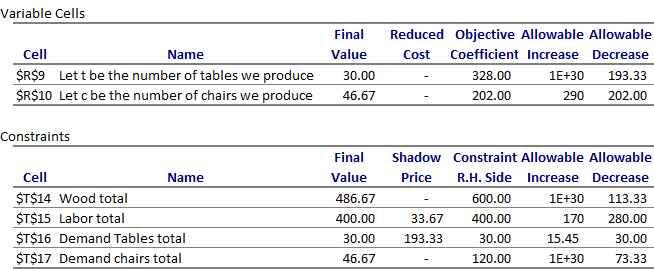
Variable Cells Section in the Sensitivity Report
What does the Reduced Cost Tell Us?
The principal values of interest in the variable cells department of the sensitivity study are the "Reduced Cost" values for each of the decision variables chosen in the linear programing model. The reduced cost value for each conclusion variable tells you how much your objective part value will modify for a i unit increase in that decision variable.
The reduced toll for decision variable A in this case is zero. Allow united states come across how we tin can translate the reduced cost if the reduced cost for the number of tables we produce was instead a negative value: -13.58. A reduced cost of -13.58, would indicate that a 1 unit increase in the final value of the tables conclusion will result in a subtract of the objective value by 13.58. The objective value in this case is profits and and then we would see a reduction in profits of 13.58 if nosotros produce one additional table.
Objective Coefficient
The Objective Coefficient is the coefficient of the decision variables in the linear programing equation that yous fix and ran on solver.
You were trying to maximize profits in this example. The profits considered the revenues and costs of machine time and material. The Objective Coefficient of 328 indicates that for each unit of decision variable A, which is the number of tables we produce in this case, your turn a profit went up by 328.
Notwithstanding, this Objective Coefficient value has not considered the opportunity cost of producing one additional unit. The reduced cost discussed above has considered the opportunity price of producing that unit too.
Allowable Increase And Allowable Subtract
The commanded increment and allowable subtract values tell yous how much the objective coefficient of a determination variable can change before the recommended solution (decision variables) will change. In other words, if the objective coefficient of conclusion A increases by an amount less than the commanded increment, the recommended solution to the model/problem (optimal decision variables) will non change. All the same if the objective coefficient increases by an amount greater than 13.58, you will see that the final value for conclusion A volition change from what is optimal now.
In this instance, you will note that the allowable increment for decision variable A (tables) is a very large number and the allowable increment for decision variable B (chairs) is 290. This indicates that the recommended decision variables will not change even if A increases past a very large amount. Whereas if the objective coefficient of decision B increases past lets say 290 units or more, the recommended solution to the model/problem (optimal decision variables) will alter.
However, if the objective coefficient decreases by 193.33 units for A or 202 units for B, you volition see that the optimal solution recommended will modify from what is recommended at present.
Constraints Department in the Sensitivity Report
The second department in a Sensitivity Written report is the Constraints section. The Constraints section of the Sensitivity Report provides you lot with the final values, the Shadow Price, the right hand side constraint and the commanded increase and decrease for each of the linear programing model's constraints.
What does the Shadow Cost Tell Us? How tin we employ the Shadow Price?
The primary values of interest in the Constraints section of the sensitivity report are the "Shadow Price" values for each of the constraints in the linear programing model. The shadow price for each constraint variable tells yous how much your objective function value volition change for a one unit increase in that constraint.
Note that we have no shadow price for wood but have a shadow price of 33.67 for labor. Notice, the constraints section, that the final value and the right hand side value of labor is 400 indicating we have used all the available labor nosotros accept. The shadow price of 33.67 for the labor in this case indicates that for every additional unit of labor we obtain will consequence in an increase of 33.67 in the objective value. This shadow price indicates our profits (objective office) will increase by $33.67 for every additional unit of labor added.
On the other hand, a shadow cost of nothing for the forest indicates that an boosted unit of wood does not increase our profits or objective function. Notice, the constraints section, that the final value of wood is 486.67 whereas the right hand side constraint is 600. This indicates that we have not used all the wood nosotros have and explains why nosotros accept a shadow price of zero! More than wood volition only add to our unused wood stockpile!
Constraint R.H. Side
The R.H. Side constraint is the correct-mitt side of that constraint equation in the linear programing model that you set up upwards and ran on solver.
You were told in the question y'all had only 600 units of wood and 400 units of labor available. In addition, you were told that the maximum number of tables demanded was thirty tables and the maximum number of chairs demanded was 120 chairs. These are the values yous find in the R.H. Side constraint.
Allowable Increment And Commanded Decrease
The allowable increase and allowable subtract values tell y'all how much the correct-hand side constraint can change earlier the shadow price becomes unreliable (or changes). In other words, if the right-manus side constraint increases by an corporeality less than the commanded increment, the shadow price will not change and is relevant. Nonetheless, if the right-manus side constraint increases by an amount greater than the allowable increment or decreases by an amount more than the allowable decrease, the shadow price changes and will not hold any more.
In this example, y'all will note that the allowable increment for labor is 170 and commanded decrease for labor is 280. This indicates that equally long every bit the labor bachelor increases by less than 170 or decreases past less than 280, the shadow price of 33.67 holds truthful. Since the shadow cost holds within this range, I tin can approximate the increase in profits if I add 10 units of labor using the shadow price and know that the profits go up past x*33.67= 336.vii! However, if the labor availability increased past 200 units, the shadow price of 33.67 will not be valid anymore. Since the shadow cost is not valid anymore, I cannot judge the increase in profits using the shadow price of 33.67.
The Respond Written report
The Answer Written report is not especially useful because most of what the Answer Written report provides will already be evident to you lot when yous look at the solver optimized model.
Your eyes volition naturally migrate to the objective cell to run across what the maximum or minimum value your target objective cell is when your solver programme has run its course. You then instinctively expect for the decision variables that volition become you the indicated objective value you were trying to maximize or minimize. You would have followed that up by trying to sympathize which of your constraints were binding or limiting you to the specified objective value. These are going to be repeated in the Answer Report!
Then on start glance, Reply Written report does not seem very useful. However, the Answer Report does layout the details more than clearly and provide you some other details that are not evident in the Excel model.
It starts by laying out the details of the linear programing model that was run. It specifies the date and time and states the results of the run. "Solver found a solution. All Constraints and optimality atmospheric condition are satisfied." Or otherwise…. The Reply Report indicates the model that was utilise: Simplex LP, GRG nonlinear or Evolutionary? The Reply Report also specifies how much time the model took, the number of iterations run and provides other options available to yous.
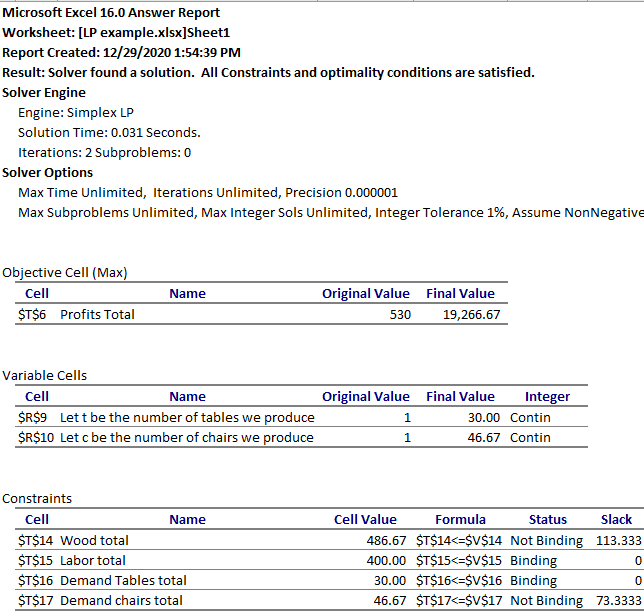
The Reply Written report then goes on to item the original value and final value of the objective function and the conclusion variables. It also specifies if the decision variables were specified to be integers, All different or binary.
The Respond Report then goes on to hash out the constraints. Here the Answer Report does non provide the original values just gives you the final values, the formula used and indicates if each constraint was bounden or not bounden. This section as well tells you if the constraint had "slack" – backlog or unused quantities of each constraint. In this case, you can come across that the labor available and need for tables are the binding or limiting constraints. Whereas, wood available and demand for chairs are "Not binding" and have slack or unused quantities available.
Limits Study in LP Solver Model
The third written report that Microsoft Excel'due south Solver add in spits out is the Limits Report. The Limits Report is not every bit useful as the Sensitivity Study.
The showtime section of the Limits Repot but provides yous with the final value of the objective function. In our example the profits you will make with the optimal solution of 30 tables and 46.67 chairs will exist $19,266.67.
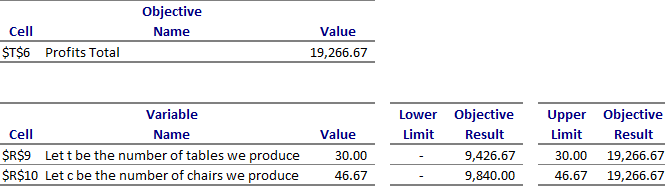
The second department of the Limits Written report is the Variable Cells department. Information technology provides you lot with the final values of the decision variables in the LP model. This section besides tells you lot what the lower limit and upper limit of the decision variables would be and what the corresponding profits will be at these lower and upper limits with no other changes made. For example we can encounter that the objective function or profits will be 9426 if we produce no tables keeping chairs constant at 46.67.
Do electronic mail or call u.s. if we can help you sympathize on translate a linear programing models output. Our operations tutors volition be glad to walk y'all through a linear programing model's sensitivity analysis, reply written report and limits report.
Source: https://www.graduatetutor.com/operations-research/interpreting-a-linear-programing-models-sensitivity-report-answer-report-limits-report/
Belum ada Komentar untuk "How to Read a Sensitivity Report in Linear Programming"
Posting Komentar